
图分为有向图和无向图,图的表示方法有两种,且都可以表示有向图或者无向图:
- 邻接链表标示
- 矩阵标示
如下图:
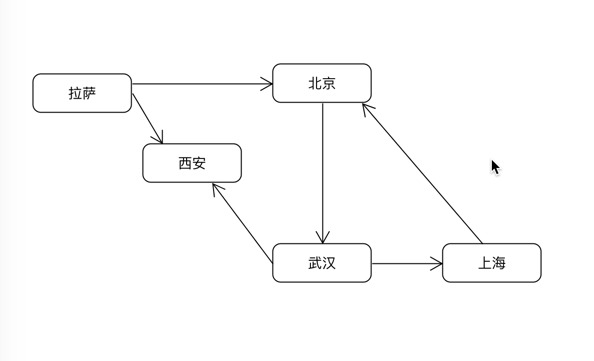
使用邻接链表标示:
北京->武汉武汉->西安->上海西安上海->北京拉萨->北京->西安
使用矩阵标示 [北京, 武汉, 上海, 西安, 拉萨]分别为 v1-v4, 1标示连通, 0标示不连通
| 0 | 1 | 0 | 0 | 0 || 0 | 0 | 1 | 1 | 0 || 1 | 0 | 0 | 0 | 0 || 0 | 0 | 0 | 0 | 0 || 1 | 0 | 0 | 1 | 0 |
使用矩阵的优点,很容易看出是否两个结点间的连通性,缺点是牺牲了存储空间
图广度优先算法,找出s源节点出发,经过最少结点到达所有结点算法:
//我们这里采用邻接链表标示图class Graph { constructor(vertexs) { this.adj = {}; vertexs.forEach( (vertex) => { this.adj[vertex] = {}; }) } addVertex(vertex) { //添加结点 this.adj[vertex] = {}; } /** * @param {Edge} edge */ addEdge(edge) { //添加边 if (!this.adj[edge.from]) { throw new Error(`vertex ${edge.from} 不存在`) } if (!this.adj[edge.to]) { throw new Error(`vertex ${edge.to} 不存在`) } this.adj[edge.from][edge.to] = edge.weight; } neighbor(vertex) { //结点vertex所有邻居结点 if (!this.adj[vertex]) { throw new Error(`vertex ${vertex} 不存在`); } return Object.keys(this.adj[vertex]); } vertexs() { //获取所有顶点 return Object.keys(this.adj); }}class Edge { constructor(from, to, weight) { this.from = from; this.to = to; this.weight = weight; }}var graph = new Graph(['北京', '上海', '武汉', '西安', '拉萨']);graph.addEdge(new Edge('北京', '武汉', 1));graph.addEdge(new Edge('武汉', '上海', 1));graph.addEdge(new Edge('武汉', '西安', 1));graph.addEdge(new Edge('上海', '北京', 1));graph.addEdge(new Edge('拉萨', '西安', 1));graph.addEdge(new Edge('拉萨', '北京', 1));/** * 算法逻辑: 最开始时先把所有结点标为白色,每次把将要遍历的结点染为灰色, * 遍历过的结点染为 黑色,当所有结点都为黑色时,遍历完成 * @param {Graph} graph * @param {vertex} s * @constructor */function BFS(graph, s) { var COLOR_WHITE = 'white'; var COLOR_GRAY = 'gray'; var COLOR_BLACK = 'black'; var vertexs = {}; //临时变量存储所有结点 //把所有结点设为白色 graph.vertexs().forEach( (vertex) => { vertexs[vertex] = {}; vertexs[vertex].color = COLOR_WHITE; vertexs[vertex].distance = Number.POSITIVE_INFINITY; vertexs[vertex].parent = null; }); //从源节点s开始遍历 vertexs[s].color = COLOR_GRAY; vertexs[s].distance = 0; //离源节点的距离 var queue = []; //充当先进先出队列 queue.push(s); while(queue.length) { let u = queue.shift(); //出列 graph.neighbor(u).forEach( (vertex) => { if (vertexs[vertex].color == COLOR_WHITE) { vertexs[vertex].color = COLOR_GRAY; //开始遍历染成灰色 vertexs[vertex].parent = u; vertexs[vertex].distance = 0; //初始化距离参数,否则为正无穷 vertexs[vertex].distance = vertexs[u].distance + 1; queue.push(vertex); //入列 } }) vertexs[u].color = COLOR_BLACK; //所有子结点及自己遍历完成,染成黑色 } return vertexs;}//求北京这个结点都所有结点最短距离:console.info(BFS(graph, '北京'));最终输出结果:{ '北京': { color: 'black', distance: 0, parent: null }, '上海': { color: 'black', distance: 2, parent: '武汉' }, '武汉': { color: 'black', distance: 1, parent: '北京' }, '西安': { color: 'black', distance: 2, parent: '武汉' }, '拉萨': { color: 'white', distance: Infinity, parent: null } }